 The largest integer that is less than 2.7 is 2. So $$\lfloor 2.7\rfloor = 2$$ .
The largest integer that is less than 2.7 is 2. So $$\lfloor 2.7\rfloor = 2$$ .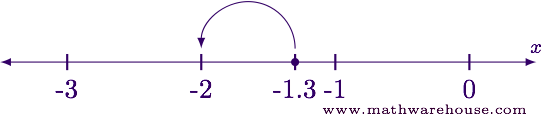 Since the largest integer that is less than -1.3 is -2, so $$\lfloor -1.3\rfloor = -2$$ .
Since the largest integer that is less than -1.3 is -2, so $$\lfloor -1.3\rfloor = -2$$ .$$\lfloor x \rfloor = \mbox$$ less than or equal to $$x$$.
In mathematical notation we would write this as
The notation "$$m\in\mathbb$$" means "$$m$$ is an integer".
Evaluate the following.
Solution
 The largest integer that is less than 2.7 is 2. So $$\lfloor 2.7\rfloor = 2$$ .
The largest integer that is less than 2.7 is 2. So $$\lfloor 2.7\rfloor = 2$$ .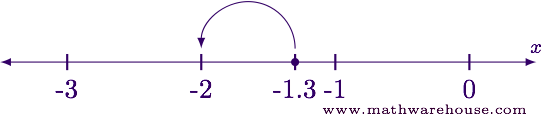 Since the largest integer that is less than -1.3 is -2, so $$\lfloor -1.3\rfloor = -2$$ .
Since the largest integer that is less than -1.3 is -2, so $$\lfloor -1.3\rfloor = -2$$ .To understand the behavior of this function, in terms of a graph, let's construct a table of values.
$$ \begin <|c|c|>\hline x & \lfloor x \rfloor\\ \hline -1.5 & -2\\ -1.25 & -2\\ -1 & -1\\ -0.75 & -1\\ -0.5 & -1\\ -0.25 & -1\\ 0 & 0\\ 0.25 & 0\\ 0.5 & 0\\ 0.75 & 0\\ 1 & 1\\ 1.25 & 1\\ 1.5 & 1\\ \hline \end $$
The table shows us that the function increases to the next highest integer any time the x-value becomes an integer. This results in the following graph.
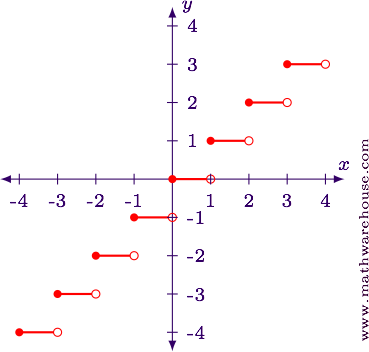
Answer
Sketch a graph of $$y = \left\lfloor \frac 1 2x \right\rfloor$$ .
We know what the basic graph should look like, so we just need to understand how the factor of $$\frac 1 2$$ is going to affect things. We can do this in two ways: we can make a table of values, or we can interpret this as a transformation.
$$ \begin \begin <|c|c|c|>\hline x & \frac 1 2 x & \left\lfloor \frac 1 2 x\right\rfloor\\[6pt] \hline -2 & -1.5 & -2\\[6pt] -1.5 & -0.75 & -1\\[6pt] -1 & -0.5 & -1\\[6pt] -0.5 & -0.25 & -1\\[6pt] 0 & 0 & 0\\[6pt] 0.5 & 0.25 & 0\\[6pt] 1 & 0.5 & 0\\[6pt] 1.5 & 0.75 & 0\\[6pt] 2 & 1 & 1\\[6pt] \hline \end \end $$
We notice from the table that the function values jump to the next value when $$x$$ is even.
We can interpret $$y = \left\lfloor \frac 1 2 x\right\rfloor$$ as a horizontal stretch which doubles the length of each piece.
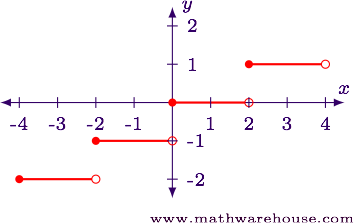
Answer:
AdvertisementThere is a formula that can help us when working with equations that involve the floor function.
$$\lfloor x\rfloor = m\qquad\mbox\quad m \leq x < m + 1$$
(remember, $$m$$ is an integer!)
So, for example, $$\lfloor x\rfloor = 8$$ if and only if $$8 \leq x < 9$$.
Solve the equation $$\lfloor 2x + 5\rfloor = 9$$ .
Rewrite the equation using the inequality.
Solve the inequality.
In interval notation, the equation is true for $$x \in [2, 2.5)$$ .
Solve the equation $$\lfloor 1.25 + \lfloor x\rfloor\rfloor = 12$$ .
Replace $$\lfloor x\rfloor$$ with $$u$$. This is called a "change of variable" and it will make the equation easier to work with.
$$ \begin \lfloor 1.25 + \lfloor x\rfloor\rfloor & = 12\\[6pt] \lfloor 1.25 + u\rfloor & = 12 \end $$
Replace the equation with one of the inequalities, where $$m = 12$$
$$ 12 \leq 1.25 + u < 13 $$Solve the inequality.
Since $$\lfloor x \rfloor$$ is an integer, the only way to satisfy the above inequalities is for $$\lfloor x \rfloor = 11$$ .
Determine the value of $$x$$.
Again, using the inequalities, we know